Fonction concave

En mathématiques, une fonction $f$ est dite concave lorsque la fonction opposée $-f$ est convexe.

Le fait que l'on préfère commencer par définir la notion de fonction convexe et d'en déduire celle de fonction concave trouve son origine dans le fait que l'on définit aisément la notion d'ensemble convexe, alors que celle d'« ensemble concave » est moins naturelle. On définit alors les fonctions convexes comme celles ayant un épigraphe convexe (les fonctions concaves ont un hypographe convexe). C'est pourquoi l'analyse convexe existe en tant que discipline des mathématiques, mais pas l'« analyse concave ».

Définitions

Cette définition est équivalente à la définition suivante :

Cette définition traduit le fait qu'un segment joignant deux points de la courbe représentative de $f$ est toujours situé sous cette courbe.

Cas des fonctions dérivables

On dispose de deux caractérisations :

On déduit de la seconde caractérisation :

que toute fonction concave et dérivable (sur un intervalle réel) est de classe C¹ ;
le corollaire suivant, fort pratique pour vérifier sans mal la concavité d'exemples spécifiques :

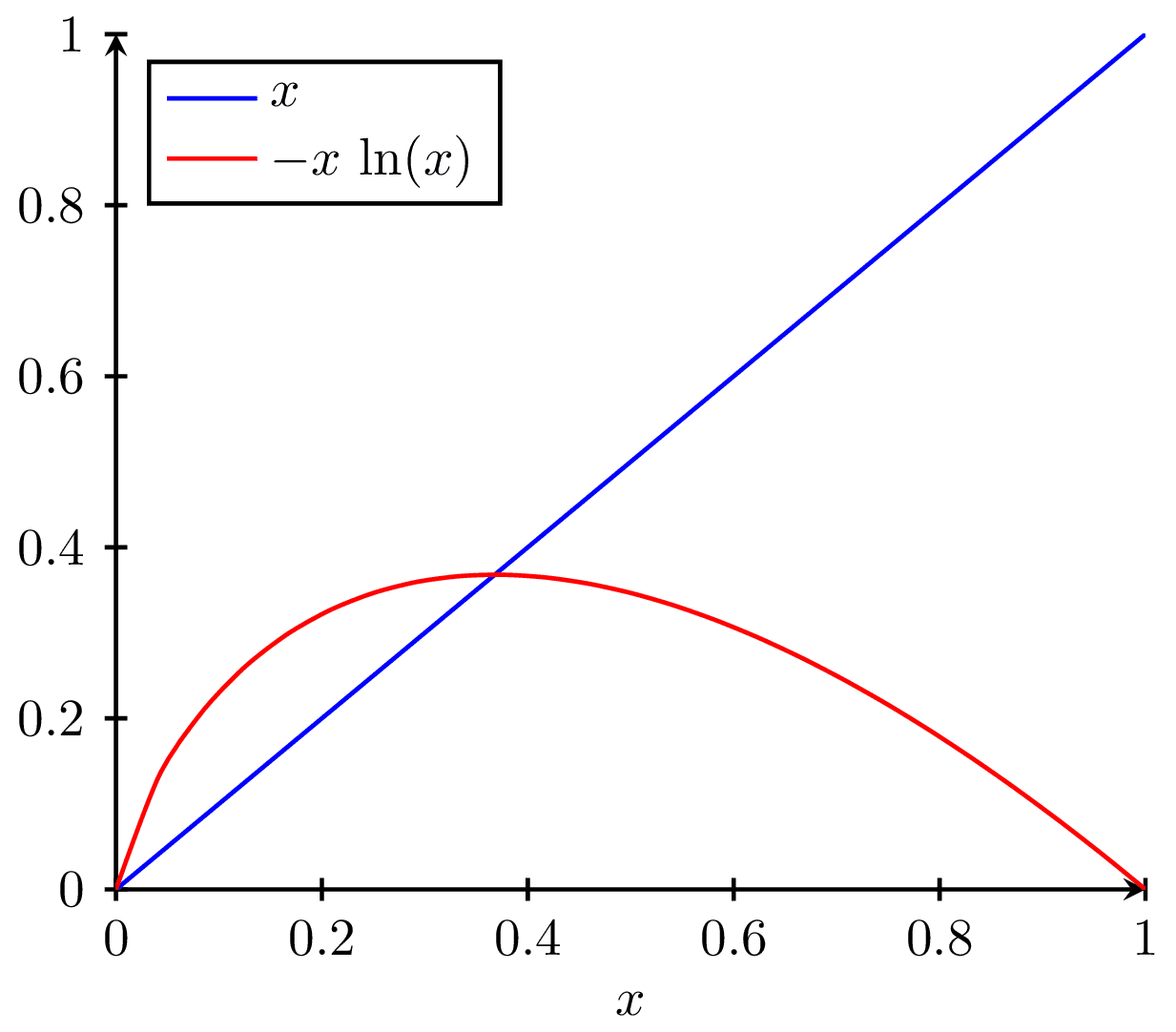
Exemple de fonctions concaves

Parmi les fonctions concaves simples, on peut citer évidemment par définition les opposées des fonctions réelles convexes, par exemple :

$x\to -x^{n}$ avec $n$ un entier pair ;
$x\to -\exp(x)$ (opposée de la fonction exponentielle).

Citons également certaines réciproques de fonctions convexes, par exemple sur $\mathbb {R} _{ }^{*}$ :

la fonction logarithme népérien $x\to \ln x$ ;
la fonction puissance $x\to x^{a}$ si $0\leq a\leq 1$ ; par exemple la fonction racine carrée $x\to {\sqrt {x}}=x^{1/2}$ .

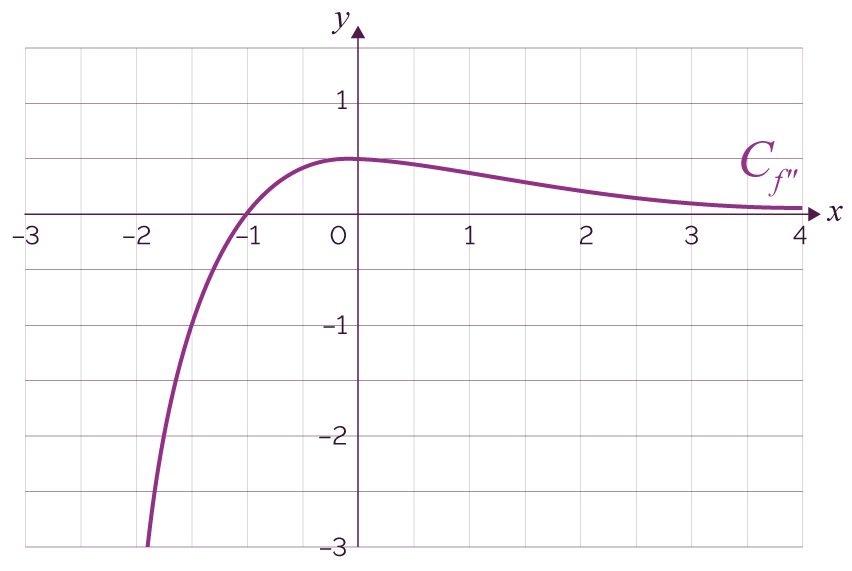
De manière plus générale, les fonctions deux fois dérivables dont la dérivée seconde est toujours négative sont des fonctions concaves. Mais une fonction concave n'est pas nécessairement dérivable, comme en témoigne la fonction $x\to -|x|$ (opposée de la valeur absolue).